波
跳至導覽
跳至搜尋



正弦波
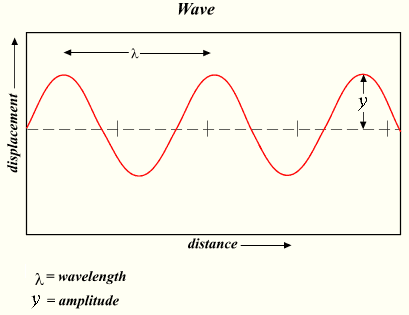
振幅

振幅(Amplitude):在波動或振動中距離平衡位置或靜止位置的最大位移。振幅屬於純量,振幅永為非負值(≥0)。
正弦波振幅的較詳細說明如下:
- 峰值振幅(U),一般稱振幅即指此
- 峰至谷振幅(2U)
- 振幅均方根(U√2,各值的平方的平均值,取平方根,用來度量一組數字的幅度,而不考慮其符號正負)
- 週期
同一位置不同時間的質點位移變化

將一個週期的時間定義為 2π ,週期內任一點的水平座標即為「相位角」(簡稱相位)。
同一位置不同時間的質點位移變化:
- y(t)=A‧sin(相位角)
- y(t+∆t)=A‧sin(相位角+∆相位角)
- 相位角=(時間長度/週期)×2π
- 相位角=ωt+φ,φ為初相角
同一時間不同位置的質點位移變化

將一個波長的距離定義為 2π ,波長內任一點的水平座標即為「相位角」(簡稱相位)。
同一時間不同位置的質點位移變化:
- y(x)=A‧sin(相位角)
- y(x+∆x)=A‧sin(相位角+∆相位角)
- 相位角=(距離/波長)×2π
不同位置不同時間的質點位移變化
綜合以上兩段:
- y(x,t)=A‧sin(相位角距離+相位角時差)
- y(x,t)=A‧sin((距離/波長)×2π+(時間長度/週期)×2π+φ)
- y(x,t)=A‧sin((距離/波長+時間長度/週期)×2π+φ)
- φ為初相角
非正弦波
固定相位角會對應固定的質點位移(否則就不是週期現象)
- ƒ 為相位角對應到其質點位移的函數
- y(x,t)=A‧ƒ(相位角距離+相位角時差)
- y(x,t)=A‧ƒ((距離/波長)×2π+(時間長度/週期)×2π+φ)
- y(x,t)=A‧ƒ((距離/波長+時間長度/週期)×2π+φ)
- φ為初相角